Por JOSÉ GUILHERME CHAUI-BERLINCK*
Um guia visual para entender o problema
A proposta deste texto é apresentar um “guia visual” que possa auxiliar uma pessoa que não seja da área dos números a entender o risco que corre ao acreditar na possibilidade de tratamentos “alternativos” (por assim dizer) no caso de se contaminar com o SARS-CoV-2 e desenvolver a COVID-19. Dada a proposta, a leitura do texto em si deve ser entendida quase que como se fosse uma grande legenda para as figuras (as quais deixo, portanto, sem legendas ). Antes de irmos, contudo, ao problema em si, penso que alguns números são importantes a serem apresentados. Então …
Alguns números preliminares
Na data atual (12 de março de 2021), temos, no mundo, 118 milhões de casos de COVID-19, contabilizando 2 milhões e 600 mil mortes. O Brasil contabiliza 11 milhões e 200 mil casos, com 270 mil mortes. A população mundial é ao redor de 7 bilhões de pessoas, a do Brasil, 212 milhões. Colocados desta maneira, estes parecem ser, apenas, números para relatos. A Figura 1 ilustra as relações de “tamanho” entre estes números.
Figura 1
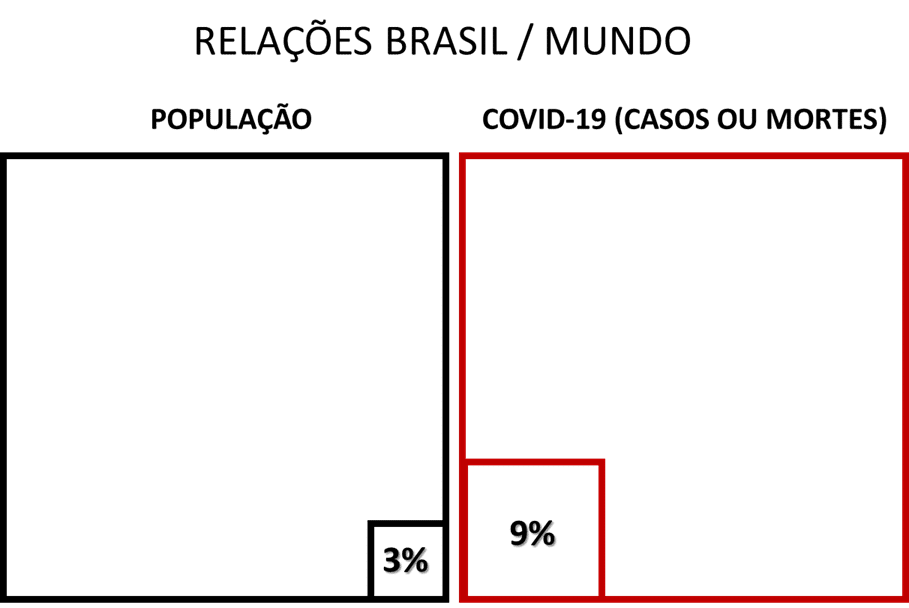
Na Figura 1 vemos que o Brasil tem uma população ao redor de 3% da população mundial, e está contribuindo (se é que este é o termo adequado) com 9% do total de casos e de mortes por COVID-19. Ou seja, o Brasil tem uma participação na atual pandemia 3 vezes maior que a que lhe caberia em proporção à sua população!
Somente este fato, vindo de números bastante simples e óbvios, deveria ser o suficiente para causar constrangimento e deflagar ações efetivas por parte dos que se apossaram do governo federal, se não por responsabilidade, ao menos por vergonha na cara.
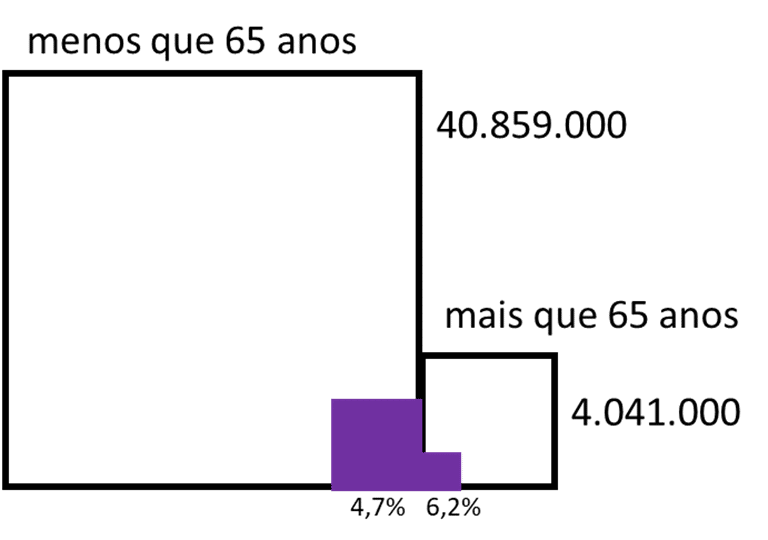
Nossos próximos números são do Estado de São Paulo[i]. A Figura 2 ilustra, em roxo, a distribuição aproximada de casos de COVID-19 nas populações abaixo e acima de 65 anos em SP. Note que há uma pequena diferença na porcentagem de casos registrados entre esses dois grupos. Os números indicam a população total de cada faixa etária. Faço essa divisão entre acima e abaixo dos 65 anos apenas para ressaltar, aos mais jovens, que os problemas que vamos discutir mais adiante não são particulares dos “idosos”. Como se verá, o pescoço de qualquer um está em jogo. A pergunta que vou deixar, ao final, é a quem você entregaria a trava da guilhotina … então, passemos ao problema.
Figura 2
 O primo médico e a pergunta errada
O primo médico e a pergunta errada
Uma pessoa, querendo se livrar do “novo anormal” para voltar ao “velho normal”, pergunta ao primo médico: se eu tiver COVID-19, devo tomar o remédio “A”?
O primo médico responde: tive quatro pacientes que tomaram e melhoraram.
A pessoa se dá por satisfeita e volta ao “velho normal”.
Isto que acabei de descrever é anedótico, porém deve ser bastante similar a fatos que você já vivenciou (se é que você não é a pessoa ou o primo médico ).
Esse remédio “A” pode ser qualquer uma das drogas ou das condutas sem qualquer respaldo técnico que vêm sendo propaladas, há tempos, por grupos de pessoas sem a mínima formação para tais afirmativas. Não importa.
O primeiro ponto que nos interessa é a pergunta da pessoa. Frente à decisão que ela teve, após a resposta, de voltar ao “velho normal”, claramente a pergunta que deveria ter sido feita não é aquela que foi. A pergunta real era: se eu tiver COVID-19 e tomar o remédio “A”, vou melhorar (ou, não vou morrer nem ficar com sequelas)?
Por que a pessoa não faz esta pergunta? O motivo da pessoa não fazer a pergunta real que ela quer fazer é porque, desta pergunta, ela já sabe quais são as respostas e a honestidade associada às respostas. Assim, uma resposta honesta que o primo pode dar é “não sei”. Não sabe pois não há tratamento (para qualquer doença) que se possa garantir 100% de eficácia. Mas “não sei”, a pessoa já sabe, e a reposta, portanto, não traz informação alguma para ela.
Por outro lado, o primo poderia responder “não”. Esta também é uma resposta honesta frente ao que se tem de estudos para estes remédios “A” que vem sendo propalados. Porém, esta resposta não permitira a volta ao “velho normal”.
Finalmente, o primo poderia responder “sim”. Contudo, ele cairia no problema de estar garantindo 100% de eficácia para um tratamento, o que tanto ele quanto a pessoa sabem não ser realista, como dissemos logo acima. Ou seja, a resposta “sim” é a resposta desonesta. Mas, é a que a pessoa quer ouvir e a que o primo quer dar. Como resolver isso?
Do mesmo modo que a pessoa transforma a pergunta real numa substituta, o primo transforma a resposta desonesta numa substituta: “tive quatro pacientes que tomaram e melhoraram”. Ele não disse “sim”. Este fica subentendido, ou, a critério do freguês decidir o que foi a resposta.
Até aqui, devo ter chovido no molhado para muitos, pois esse foi meramente um exercício de teoria da informação, estatística bayesiana e psicologia barata. O que vou procurar fazer, agora, é ilustrar, visualmente, o problema proposto pela pessoa e o alcance que a reposta pode ter. Além disso, vou procurar colocar quais são as perguntas que se pode fazer, e o que fica implícito na pergunta.
Vamos supor, agora, que a pergunta “se eu tiver COVID-19, devo tomar o remédio “A”?” esteja sendo usada de maneira honesta, ou seja, sem que esteja substituindo uma outra para a qual a pessoa já saiba o conjunto de repostas honestas que poderiam ser dadas (e que ela não quer ouvir ). O que esta pergunta quer dizer, ou ao que ela se refere?
A pergunta pode ser entendida de três formas diferentes:
- Qual a probabilidade do tratamento TA ser a causa da melhora M? ou, dado que foi feito o tratamento TA, qual a probabilidade de melhora M?
- Dado que houve melhora M, qual a probabilidade de ter recebido o tratamento TA?
- Dado que não foi feito o tratamento TA, qual a probabilidade de melhora M?
A maioria das pessoas talvez ache que a pergunta faz alusão somente ao caso 1 acima, mas as três interpretações são igualmente válidas. De fato, a resposta do primo nos induz à formulação 1.
Mas, ele poderia ter dito “conheci dois pacientes que não tomaram “A” e morreram”. Note que, agora, é a formulação 3 que está sendo acessada.
A formulação 2 é a mais complicada e dificilmente o primo vai buscar uma resposta que faça alusão a ela. Os números que foram dados nas outras respostas do primo (“quatro pacientes” e “dois pacientes”) são fáceis de serem transpostos, pelo interlocutor, em alguma “probabilidade” tangível de ser entendida. Contudo, a formulação 2 exige uma inversão do raciocínio e qualquer número dado não é auto evidente.
Entretanto, se as três formulações são válidas como equivalentes à pergunta não formal que foi feita, isso significa que para esta pergunta ser adequadamente respondida temos que conhecer a resposta para as 3 formulações que podem ser equivalentes à tal pergunta. Vou falar, então, …
… de uma doença qualquer …
Vamos imaginar uma doença que tenha surgido e não se tenha nenhum tratamento para ela. A Figura 3 ilustra a distribuição de casos e de melhora espontânea (já que, por enquanto, somente há melhora sem tratamento). A área delimitada pela linha verde indica os casos que têm melhora espontânea dentro do total de casos que se observa, delimitados pela linha vermelha. Então, alguns tratamentos surgem, e passamos para o quadro ilustrado na Figura 4. Supomos que os tratamentos não interfiram na taxa de cura espontânea e, assim, a região delimitada pela linha azul surge, expandindo o número de melhoras.
Vamos ver “quem” habita cada região da representação gráfica desta doença (Figura 5):
α: a região delimitada pela linha verde é a já conhecida desde a Figura 3, habitada por aqueles que vão melhorar com ou sem tratamento;
β: entre a região delimitada pela linha verde e a delimitada pela linha azul, habitam aqueles que antes iriam a óbito, mas agora, graças aos possíveis tratamentos, melhoram;
γ: entre a delimitação azul e a vermelha, ficam aqueles que irão a óbito, com ou sem tratamento (note que não estou dizendo que o tratamento foi a causa do óbito, estou dizendo que qualquer tratamento, se dado, é ineficaz para debelar a doença nestes indivíduos)
 |
Figura 3 |
 |
Figura 4 |
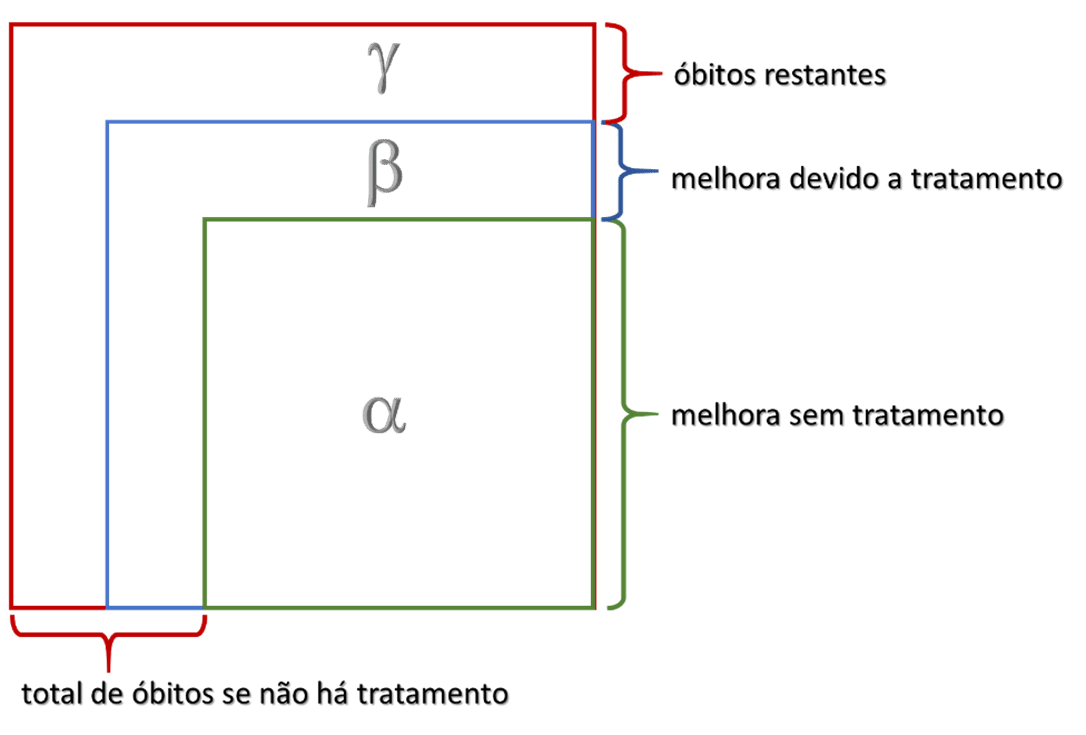 |
Figura 5 |
Note que a resposta “tive quatro pacientes que tomaram e melhoraram” induz você a considerar que o tratamento com “A” é o que cria a região b, mas esta região é habitada por todos os indivíduos que receberam algum tratamento, seja “A” ou não.
Já a resposta “conheci dois pacientes que não tomaram “A” e morreram” induz você a pensar que a região g é habitada somente por aqueles que não tomaram “A”, quando, na verdade, esta região é habitada por indivíduos que não tomaram “A”, indivíduos que tomaram “A” e indivíduos que não tiveram tratamento algum e não pertenciam ao grupo a.
Se ignorarmos as induções feitas pelas respostas, vemos que há duas questões que não foram respondidas:
- Quantos dos quatro pacientes que tomaram “A” pertenciam ao grupo a? Os que pertenciam a este grupo iriam melhorar apesar de qualquer tratamento. Veja como a seguinte resposta muda completamente a indução feita, apesar de conter a mesma afirmativa anterior: “tive quatro pacientes que tomaram e melhoraram e tive quatro para os quais não dei nada e melhoraram”.
- Quantos pacientes receberam “A” e se encontram no grupo g? Estes pacientes são aqueles para os quais o tratamento é ineficaz. Veja como a seguinte resposta muda completamente a indução feita, apesar de conter a mesma afirmativa anterior: “conheci dois pacientes que não tomaram “A” e morreram e dois que tomaram “A” e morreram”.
Neste quadro simplificado, porém suficientemente geral para não perder a validade da análise que estamos fazendo, o problema científico da validação de um certo tratamento é o de diferenciar os tratamentos quem ampliam a faixa b daqueles que nada fazem. Lembre-se que estamos desconsiderando, justamente para simplificar, a possibilidade de um certo tratamento deslocar um individuo do grupo a para o g (ou seja, o tratamento se tornar a causa da morte), e também a concomitância de tratamentos (ou seja, o tratamento “A” sendo dado junto a “B”, ou “C”, etc.).
Das 3 formulações que eu disse serem equivalentes à pergunta não formal “se eu tiver COVID-19, devo tomar o remédio “A”?”, podemos ver, na Figura 5, que somente se apenas o tratamento “A” existir é que se consegue ter respostas diretas para as formulações 1, 2 e3: a formulação 3 é a região a; e as formulações 1 e 2 seriam a mesma formulação[ii] e a resposta seria a região b.
Contudo, é aí que fica grande parte do problema a ser resolvido: uma vez que há uma multiplicidade de tratamentos que são dados concomitantemente (até por razões éticas), como diferir a participação de cada um no desfecho final? Ou seja, quais tratamentos ampliam a região b e quais não.
Este problema científico não é resolvido com 2, 4, 6, ou 20 pacientes que um médico tenha visto. Essa é a vivência do profissional, mas não é a experiência de validação de um tratamento.
As populações contidas nas áreas representadas nas figuras são enormes, na ordem de milhares e, no caso da COVID-19, estamos na ordem de centenas de milhões ao redor do mundo.
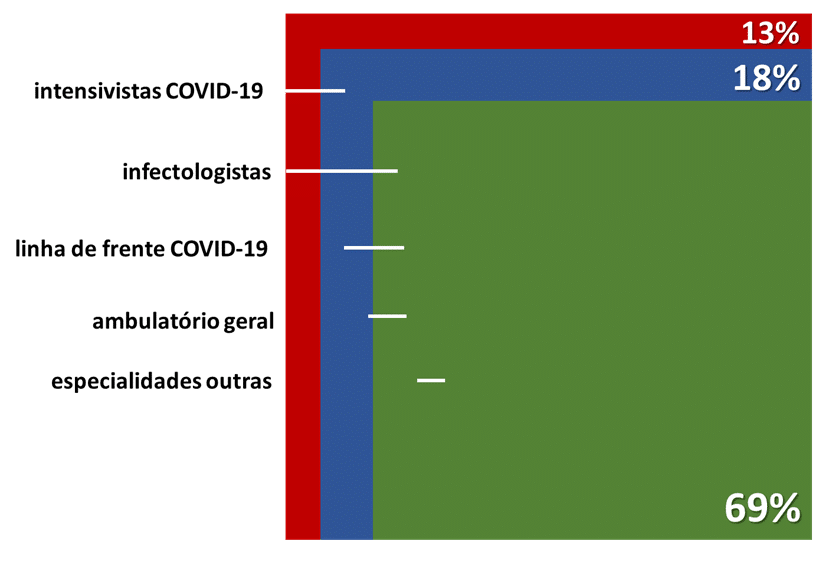
A Figura 6 ilustra, sem maiores pretensões, quais especialistas lidam com quais pacientes COVID-19. As linhas brancas indicam quais os tipos de pacientes esses especialistas veem. O ponto importante a ser percebido é que “ambulatórios gerais” e “especialidades outras”, cujos profissionais não fazem parte da linha de frente, verão, basicamente, pacientes COVID-19 do nosso grupo a. Ou seja, são profissionais que estão em contato, apenas, com o grupo que irá melhorar apesar do tratamento. É importante notar que a grande maioria dos médicos e profissionais de saúde se encontram nesta condição: contato periférico com pacientes COVID-19.
Além disso, vemos que a região b, aquela que contém os indivíduos que necessitam de tratamento adequado para não ir para a região g (óbito), compõe, aproximadamente, 20% da área[iii]. Isso quer dizer que 1 em cada 5 pessoas que contraem a COVID-19 estará nesta região b (claro que sem saber, pois não há nada que indique, previamente, quem estará em qual das regiões).
Figura 6
Tratamentos adequados
Como disse acima, não são 2 ou 20 pacientes vistos por um profissional que perfazem um grupo de teste clínico. Como também eu disse, esse tipo de circunstância é a mera vivência do profissional. Não somente um estudo precisa contar com muitos e muitos casos para se formar uma estatística adequada, como precisa ser bem delineado em termos de grupos e tratamentos. Portanto, qual é o quadro atual (março de 2021) que se tem em termos de recomendações de tratamento para COVID-19? Ou, utilizando o vocabulário que criamos mais acima, quais são os tratamentos medicamentosos considerados adequados para colocar indivíduos da região g na região b?
A tabela abaixo é baseada nos guias de tratamento de COVID-19 feitos pela Sociedade Americana de Doenças Infecciosas (IDSA[iv]), Institutos Nacionais de Saúde estadunidenses (NIH) e Organização Mundial de Saúde (OMS). Nela eu listei apenas as drogas mais propaladas pelos grupos aos quais me referi anteriormente, e corticosteroides. Uma simples leitura da tabela já permite perceber quais podem fazer e quais não vão fazer o indivíduo sair da região g e ir para a região b.
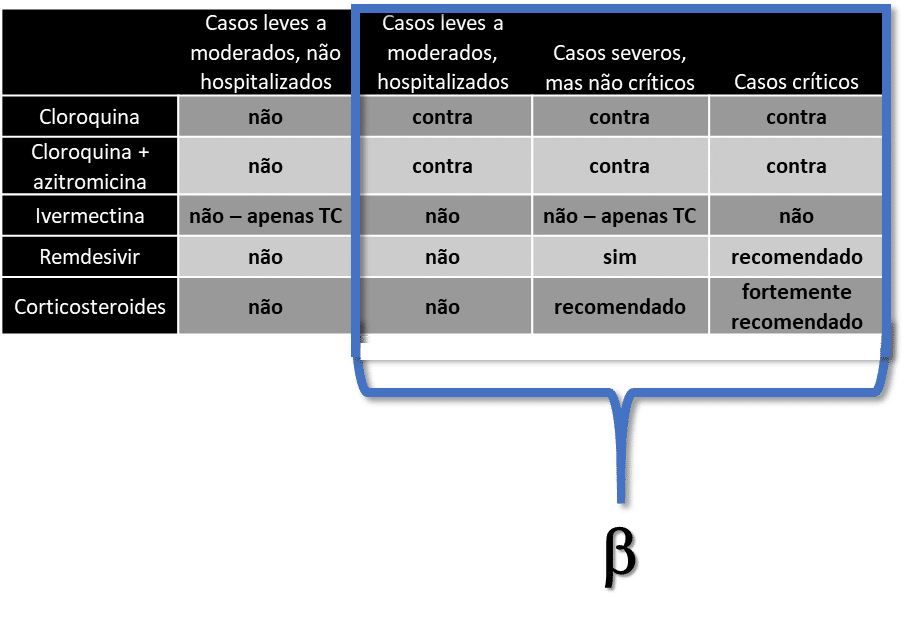
TC: testes clínicos
E se fosse você?
Finalmente, chegamos à questão que anunciei lá no início.
A Figura 7 corresponde aos quadrados roxos da Figura 2, utilizando o padrão de cores das figuras anteriores para discriminar entre os grupos a, b e g (veja as Figuras 5 e 6). Imagine que você seja um dardo a ser jogado, aleatoriamente (pois você não sabe, a priori, a que grupo pertence), na Figura 7.
Se você cair na região verde, salva-se apesar de qualquer tratamento[v]. Se cair na região vermelha, sinto muito, não há ou havia o que fazer por você.
O dardo pode ir parar, ainda, na região azul, correspondente ao grupo b. Vimos que a chance disso acontecer está por volta dos 20% (1 em cada 5).
E aqui vem a grande questão: se o seu dardo cair na região azul, aquela que depende de tratamento correto, você colocaria a sua vida no dardo imprudente jogado pelo primo?
Em outras palavras, se você está na região azul, utilizaria o tratamento sugerido pelos inconsequentes que somente veem pacientes que estão na região verde?
Figura 7

*José Guilherme Chaui-Berlinck é médico e professor livre-docente do Departamento de Fisiologia do Instituto de Biociências da USP.
Notas
[i] Tomei o Estado de São Paulo como exemplo apenas por facilidade de obter os dados. O quadro, em termos gerais, é semelhante no Brasil e a análise que nos importa não é exatamente a da precisão destes números.
[ii] A título de formalização, as formulações 1 e 2 são, respectivamente, P( M | T ) e P( T | M ). Existindo somente o tratamento TA (ou seja, T = TA) as probabilidades se tornam as mesmas.
[iii] Os números foram obtidos a partir dos dados atuais do Estado de São Paulo. A discriminação da faixa b entre os casos com melhora foi obtida a partir da fração de pacientes que necessitam cuidados médicos além dos de nível ambulatorial (consulta em 12/mar/21: https://www.uptodate.com/contents/coronavirus-disease-2019-covid-19-clinical-features?topicRef=126981&source=related_link)
[iv] https://www.idsociety.org/practice-guideline/covid-19-guideline-treatment-and-management/
[v] O que sabemos não ser verdadeiro, pois há tratamentos, principalmente aqueles do tipo “A”, com sérias possibilidades de efeitos colaterais graves.