Por JOSÉ GUILHERME CHAUI-BERLINCK*
Uma revisão da literatura científica e um panorama da situação do Brasil no quadro mundial.
O presente texto foi elaborado com o intuito de apresentar o que se tem como conhecimento científico, no presente momento, acerca da propagação do SARS-CoV-21. A data é a segunda quinzena do mês de maio de 2020. As revisões e artigos científicos aqui apresentados têm, como tema comum, as possíveis rotas de propagação do vírus. Além desta revisão da literatura científica, apresento um panorama da situação do Brasil no quadro mundial, como, também, um breve e simplificado tutorial acerca de modelos em epidemiologia, com o intuito de fornecer ferramentas básicas para a interpretação dos dados por aqueles que não têm trânsito na área. Por último, deixo algumas referências bibliográficas específicas que podem ser de interesse para a leitura. O esquema do texto se encontra abaixo.
Aspectos da transmissão do SARS-CoV-2: as possíveis rotas
Gastrointestinal e fecal-oral
Cipriano e colaboradores, em uma meta-analise feita no início de março do corrente ano, indicam que a contaminação fecal-oral deve ser considerada uma rota possível de transmissão do vírus (Cipriano et al., 2020). Pan e colaboradores (Pan et al., 2020) relatam que em 17 pacientes testados para SARS-CoV-2 nas fezes, 9 apresentaram cargas virais detectáveis (porém mais baixas que em vias aéreas). Os autores recomendam cuidado no manuseamento de amostras fecais, porém não citam a contaminação fecal-oral como rota.
McDermott e colaboradores (McDermott et al., 2020), por outro lado, considerando a propagação conhecida de SARS-CoV-1 através de aerossóis de descarga sanitária, consideram que esta seja uma possível rota de transmissão, sendo importante, principalmente, em ambientes hospitalares e similares. As descargas formam aerossóis com gotas menores que 3 mm que podem ser inaladas indo até vias aéreas respiratórias (bronquíolos terminais). Assim, os autores sugerem que pesquisas devam ser direcionadas a este tópico e que enquanto não há resultados que contradigam a hipótese, deve-se ter em mente esta possível rota de transmissão e os devidos cuidados devem ser tomados preventivamente (Wong et al., 2020).
Ainda neste tópico, Li e colaboradores (Li et al., 2020) comparam CoVs com norovirus (NoVs), estes últimos de transmissão por alimentos. Os autores apontam que os CoVs permanecem com potencial infectante após dias a semanas em alimentos, mas os autores supõem que esta não é uma rota de infecção relevante. Deng e colaboradores constatam, em macacos Rhesus, que a inoculação ocular pode causar sintomas pulmonares brandos, e que a inoculação pelo trato gastrointestinal não causa infecção(Deng et al., 2020).
O SARS-CoV-2 se liga a receptores da enzima de conversão da angiotensina tipo-2 para injetar seu material nucleico nas células hospedeiras. Assim, tanto Xiao e colaboradores quanto Lamers e colaboradores demonstram que o trato gastrointestinal, com a presença abundante de receptores da enzima de conversão da angiotensina tipo-2, é uma rota tanto para propagação quanto para infecção por SARS-CoV-2 (Lamers et al., 2020; Xiao et al., 2020).
Dada a possibilidade da rota fecal-oral de transmissão, numa meta-análise publicada em 28 de abril, La Rosa e colaboradores estudaram a propagação de coronavirus (geral) pela água (La Rosa et al., 2020). Os autores apontam que os coronavirus parecem ser extremamente sensíveis a agentes oxidantes, como cloro, e são significativamente inativados mais rapidamente que outros vírus de conhecida transmissibilidade pela água. A meta-análise aponta que não há evidência da persistência de coronavirus em águas nem de transmissão por água contaminada.
Em conclusão, a rota fecal-oral é uma possibilidade aberta para a transmissão do SARS-CoV-2. Contudo, não há, até o presente momento, nenhuma evidência quanto a haver casos originados por tal rota. Por outro lado, a transmissão por aerossóis decorrentes de águas contaminadas por fezes contendo SARS-CoV-2 deve ser seriamente levada em consideração.
Superfícies e temperaturas
O tempo de persistência de coronavirus em geral em superfícies é de 5 a 9 dias (Fiorillo et al., 2020), e o tempo de persistência de SARS-CoV-2 é um pouco menor (dependendo do tipo de superfície, por exemplo, cobre tem potencial de inativar os vírus em 4 horas) (van Doremalen et al., 2020).
Christophe Batéjat et al. (versão postada em 1º de maio de 2020 – bioRxiv preprint doi: https://doi.org/10.1101/2020.05.01.067769 – Heat inactivation of the Severe Acute Respiratory Syndrome Coronavirus 2), através da estimativa de TCID50 (dose infectante de 50% da cultura tecidual), apresentam dados que indicam que o SARS-CoV-2 é inativado em 30 minutos a 56 oC, 15 minutos a 65 oC e 3 minutos a 95 oC (notam, no entanto, que o RNA viral persiste intacto nas partículas, mesmo inativadas).
Apesar deste grande tempo de persistência das partículas viriais em superfícies (fômites2), ainda não houve evidências observacionais ou experimentais de que esta via de contaminação tenha sido responsável por casos em ambientes não hospitalares (ver secção “Resumo”, mais abaixo).
Em conclusão, aparentemente, o SARS-CoV-2 pode ser inativado em temperaturas ao redor de 60 oC a 70 oC por um par de dezenas de minutos, e não se deve confundir a persistência do RNA viral com a capacidade infectante da partícula.
Aerossóis
Aerossol é a denominação que se faz para gotículas líquidas de tamanho muito pequeno (isto será um pouco mais detalhado no texto adiante).
“Ainda hoje, surpreendentemente, a literatura é indecisa sobre como a gripe se espalha em relação a gotículas versus transmissão aérea [aerossól]. Essa discussão é notável, pois não há dúvida de que a gripe é altamente infecciosa e transportada pelo ar; após meu próprio compartilhamento de carro como estudante de medicina, sentindo os primeiros estágios de uma gripe. Sugeri aos dois companheiros que pegassem um trem, mas eles insistiram em entrar no carro. Não houve tosse, espirro ou mesmo conversa, simplesmente respirando o mesmo ar por meia hora e os dois caíram com gripe severa dois dias depois. Portanto, haverá risco variável, dependendo do tempo de exposição, ventilação da área e quantidade de vírus circulando. Sem conhecer esses parâmetros, o risco de infecção pode ser alto ou baixo.” (Barr, 2020) – tradução livre.
Segundo (Hsiao et al., 2020), a diferenciação dicotômica feita pela Organização Mundial da Saúde entre “gotículas” e “aerossóis” (“droplets” e “airborne”) causa problemas interpretativos consideráveis quando se faz referência às rotas possíveis de disseminação de patógenos. A diferenciação se dá pelo tamanho das partículas, sendo as gotículas maiores e “molhadas”, enquanto, os aerossóis, pequenos e, devido à evaporação da água originalmente presente ao lançamento do material, secos. Desta maneira, e devido aos tamanhos diferentes, as gotículas tendem a cair pela ação da gravidade e têm um tempo de permanência no ar bem menor que o material particulado originado pelos aerossóis. Por outro lado, a persistência de patógenos ativos, em geral, tende a ser menor no particulado seco que nas gotículas, e são estas últimas que, devido à queda, se assentam sobre superfícies ou o próprio chão, enquanto os aerossóis permanecem suspensos no ar por horas ou dias.
Num artigo publicado em 17 de março, van Doremalen e colaboradores mostram que o período médio de persistência do SARS-CoV-2 em aerossóis é de 3 horas, com características similares ao do SARS-CoV-1 (van Doremalen et al., 2020). Este artigo tem sido alvo de inúmeras citações, tanto para tê-lo como evidência da necessidade de se tomarem precauções contra o contágio por aerossóis quanto para critica-lo em relação à realidade da disseminação do SARS-CoV-2 por esta via.
Por exemplo, Peters e colaboradores (Peters et al., 2020) procuram dar um quadro mais realista à questão da semelhança entre o experimento de van Doremalen et al. e partículas criadas em situações reais pela fala, tosse ou respiração, apontando que existe uma diferença muito grande entre o experimento com o tambor de Goldberg (ver Figura 1, abaixo) e aquilo que é fruto destas atividades humanas. Vários outros autores comentam acerca da distinção necessária entre o experimento e a possível rota de contaminação (há muitos artigos e cartas neste sentido, assim, apenas deixo o DOI do New England Journal of Medicine com uma série destas para quem tiver interesse: “Stability and Viability of SARS-CoV-2” – DOI: 10.1056/NEJMc2007942).
Pode-se, assim, resumir as críticas a dois planos: (1) não existe uma paridade entre o observado experimentalmente num tambor de Goldberg e aquilo que ocorre num ambiente não artificial de experimentação; (2) o quanto se deve investir, numa situação de escassez, em equipamentos mais refinados de prevenção da contaminação por aerossol sem que haja uma evidência mais sólida acerca da viabilidade desta rota (é importante notar que os autores do artigo original nunca afirmaram nada quanto a estes dois itens). Dentro desta perspectiva, em um artigo de meta-análise do começo de abril/2020, Tabula conclui que não há evidências para supor os aerossóis como via de contaminação (Tabula, Joey. “Is SARS-CoV-2 transmitted by airborne route?.” – Asia Pacific Center for Evidence Based Healthcare).
Contudo, vários outros artigos têm sido publicados num viés oposto. Morawska & Cao chamam a atenção para a disseminação por aerossol como importante rota para infecção, principalmente em ambientes restritos (Morawska and Cao, 2020). Hadei e colaboradores concordam que as evidências da transmissão de SARS-CoV-2 por aerossóis não são completas, porém que os achados observacionais são altamente sugestivos e, assim, consideram que o uso preventivo de máscaras se justifica (ver próxima secção) (Hadei et al., 2020). Em um artigo recente, de 11 de maio, Dancer e colaboradores3 voltam a insistir que a rota de disseminação por aerossol deve ser considerada como real, citando ao menos dois incidentes nos quais este tipo de espalhamento tem que ter sido o responsável pelos casos que surgiram (Dancer et al., 2020). Além de apresentar estes dois eventos emblemáticos, os autores apontam o problema da distinção binária que se faz entre “gotículas” e “aerossóis”, como levantado mais acima nesta secção. Ainda neste viés de evidências observacionais, Galbadage et al. consideram que a disseminação via aerossol é real para o SARS-CoV-2 e que, entre outras medidas preventivas já estabelecidas, o uso de máscaras se faz importante (ver próxima secção) (Galbadage et al., 2020).
Resumo dos tópicos acerca das rotas de transmissão do SARS-CoV-2
Me parece que a meta-análise feita por Brurberg, em 7 de maio, serve como resumo do estado atual de conhecimento acerca das vias de contaminação do SARS-CoV-2, e transcrevo a conclusão da análise:
“Rastreamento de transmissão e rotas prováveis de transmissão
Foram incluídos oito estudos de rastreamento de transmissão. Todos os estudos concluem que a transmissão geralmente ocorre entre pessoas que estão em contato próximo, mas um estudo relata alguns casos em que a transmissão pode ter ocorrido através de superfícies inanimadas contaminadas. Esses resultados podem ser tomados como indicação de que o SARSCoV-2 é transmitido na comunidade por uma combinação de gotículas, contato direto e indireto. Os estudos não foram projetados para diferenciar várias vias de transmissão e são inconclusivos quanto à importância relativa de várias vias de transmissão na comunidade.” (Brurberg, 2020) – tradução livre.
Máscaras
Abordagem empírica/observacional
Pode-se estimar entre 50% a 80% de pessoas sendo portadoras assintomáticas do SARS-CoV-2, como citado por (Esposito et al., 2020), e que a carga viral transmitida por estes indivíduos se assemelha às dos sintomáticos. De acordo com estes autores, originalmente se acreditava que a transmissão somente ocorreria por gotículas originárias por tosse/espirro, há, agora, evidências de que (1) o SARS-CoV-2 se encontra presente e com potencial infectante em aerossóis (van Doremalen et al., 2020), (2) o simples ato de falar produz descarga de aerossóis (Anfinrud et al., 2020). Desta maneira, os autores sugerem que o uso de máscaras, mesmo que de baixa eficácia como as feitas-em-casa, seja adotado como medida complementar ao isolamento social e cuidados de higiene. Ainda nesta linha, o estudo de (He et al., 2020) sugere que a principal fase de transmissão ocorra durante o período pré-sintomático.
Anderson et al. discutem, inicialmente, a problemática da divisão binária entre “gotículas” e “aerossol”, a qual leva a separações artificiais entre os possíveis meios de transmissão do SARS-CoV-2 (Anderson et al., 2020). Em seguida, a partir de uma perspectiva de análise de risco (que lida com informações científicas incompletas), os autores apontam 3 linhas de evidência quanto à propagação do vírus por aerossóis: (1) casos reportados de pessoas assintomáticas tendo sido o foco transmissor a outros indivíduos; (2) amostras de SARS-CoV-1 e SARS-CoV-2 em aerossóis tanto em coletas empíricas em ambientes hospitalares quanto em experimentos; (3) propagação, via aerossol, de outros patógenos. Os autores concluem que existe uma necessidade urgente em se definir as possíveis rotas de transmissão do SARS-CoV-2 e que o uso de “protetores inalatórios” tem evidência suficiente para ser adotado.
Barr (Barr, 2020), citado na abertura da secção anterior, não somente preconiza o uso generalizado de máscaras como, ainda, sugere que cada pessoa deva ter três máscaras para revezamento diário (dado que a informação que se tem acerca da persistência de SARS-CoV-2 em máscaras é de 3 dias – (Chin et al., 2020)).
Como entender o aparente seguinte paradoxo? As máscaras cirúrgicas não têm a eficácia filtrante dos chamados respiradores (máscaras de bom ajuste à face e com filtro – geralmente N95 que reduz em 95% a inalação de aerossóis maiores que 3 mm de raio), porém países que adotaram o uso disseminado de máscaras, mesmo apenas cirúrgicas ou caseiras, registraram intensa queda na propagação do SARS-CoV-2. O que Hsiao e colaboradores propõem é que as máscaras, mesmo as mais simples e com baixa a baixíssima capacidade filtrante, têm o importante papel de redução na velocidade do ar expelido, seja em episódios de tosse/espirro, seja em conversas ou apenas na respiração normal. Com esta diminuição da velocidade, o alcance imediato dos aerossóis e gotículas expelidos se reduz acentuadamente4 e, desta forma, há uma diminuição da probabilidade de transmissão do vírus (Hsiao et al., 2020).
Abordagem teórica
O modelo básico que se emprega para o estudo de propagação de epidemias é o de uma população de indivíduos susceptíveis à doença em foco, geralmente denotados pela letra S, um conjunto de indivíduos infectados, geralmente denotados por I, que, com a resolução da doença, se tornam recuperados, denotados por R. Um indivíduo pertencente ao grupo S passa ao grupo I devido ao contato com algum individuo do grupo I (isto é a transmissão da doença), e um individuo do grupo I passa ao grupo R em decorrência do tempo para a cura da infecção. Este é um dito modelo SIR, que pode ser, então, tornado extremamente complexo com a adição de “estruturas” na população – por exemplo, divisão em idades, em portadores assintomáticos, em indivíduos com doenças prévias, etc.- e/ou pela adição do espaço como outra variável – ou seja, as localizações dos indivíduos tomam parte no modelo5. Quando o espaço não é levado em conta de maneira explícita, o modelo é dito “compartimental”, e estes podem ter soluções analíticas (ou seja, pode-se conseguir determinar se, por exemplo, uma doença será erradicada da população ou permanecerá como uma endemia), dependendo da quantidade de equações que se tem no modelo. A última secção do presente texto apresenta um breve tutorial acerca de modelos em epidemiologia.
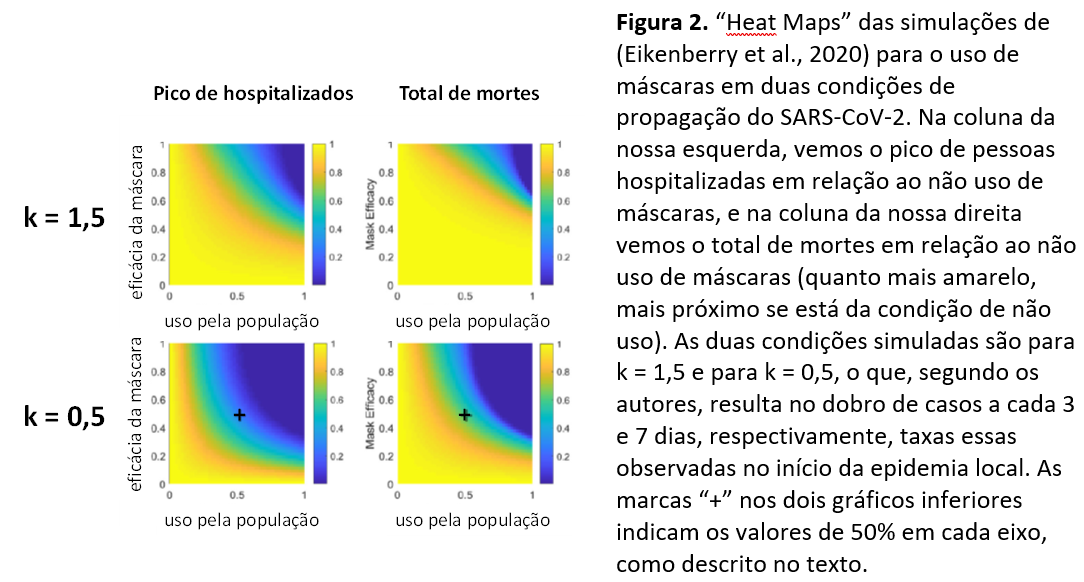
O estudo de Eikenberry e colaboradores é composto por 14 equações diferenciais e modela o uso de máscaras com diferentes eficácias por pessoas infectadas, por assintomáticos e por susceptíveis, em diferentes graus (Eikenberry et al., 2020). A Figura 2 ilustra parte dos resultados do modelo, realçando que o uso de máscaras, mesmo que as de não grande eficácia e mesmo que não por toda a população, tem grande potencial de redução tanto na quantidade de pessoas hospitalizadas quanto de mortes, sendo que tal efeito é mais acentuado em taxas de propagação menores (como as observadas após os dias iniciais dos surtos em cada localidade). Por exemplo, se 50% da população utilizar máscaras com 50% de eficácia, estima-se uma diminuição de 50% nas mortes (para k = 0,5). Note, no entanto, que para k = 1,5, a diminuição no pico de pacientes hospitalizados é pequena e irrisória na diminuição no total de mortes.
Este parâmetro, k, é o índice de transmissão da doença, e é indicado, indiretamente, pela taxa de crescimento no número de casos a cada dia (ver a secção “Um Breve Tutorial …” mais adiante). O isolamento social é, até o momento, a única medida que se conhece para diminuir o valor de k nesta pandemia por SARS-CoV-2. Desta forma, este estudo de Eikenberry e colaboradores não somente ressalta a relevância no uso de máscaras como, ainda, a necessária quarentena ou distanciamento social para a contenção da pandemia.
Numa outra modelagem acerca do uso de máscaras, feita através de um modelo compartimental e através de um modelo ABM6, (Kai et al., 2020) concluem: “Nossos modelos SEIR e ABM sugerem um impacto substancial do uso universal e precoce de mascaras. Sem tal uso, mas mesmo com o distanciamento social continuado após o encerramento do lockdown, a taxa de infecção aumentará e quase metade da população será afetada.”
Note, assim, como esses resultados teóricos vão ao encontro das observações de (Hsiao et al., 2020) colocadas anteriormente e das recomendações citadas anteriormente para o uso de máscaras pela população em geral.
Em conclusão, tanto estudos observacionais quanto experimentais e teóricos apontam, fortemente, que o uso de máscaras é um fator complementar de grande importância para a contenção da propagação do SARS-CoV-2.
Como está o Brasil na segunda semana de maio?7
Para que se possa ter uma perspectiva adequada do quadro geral no qual o Brasil se insere, é preciso que tenhamos claras quais perguntas queremos responder, e quais comparações nos parecem adequadas.
Fontes dos dados: https://www.worldometers.info/coronavirus/#news ; https://data.humdata.org/dataset/novel-coronavirus-2019-ncov-cases
Pergunta 1: o número de casos confirmados no Brasil é significativo no panorama mundial?
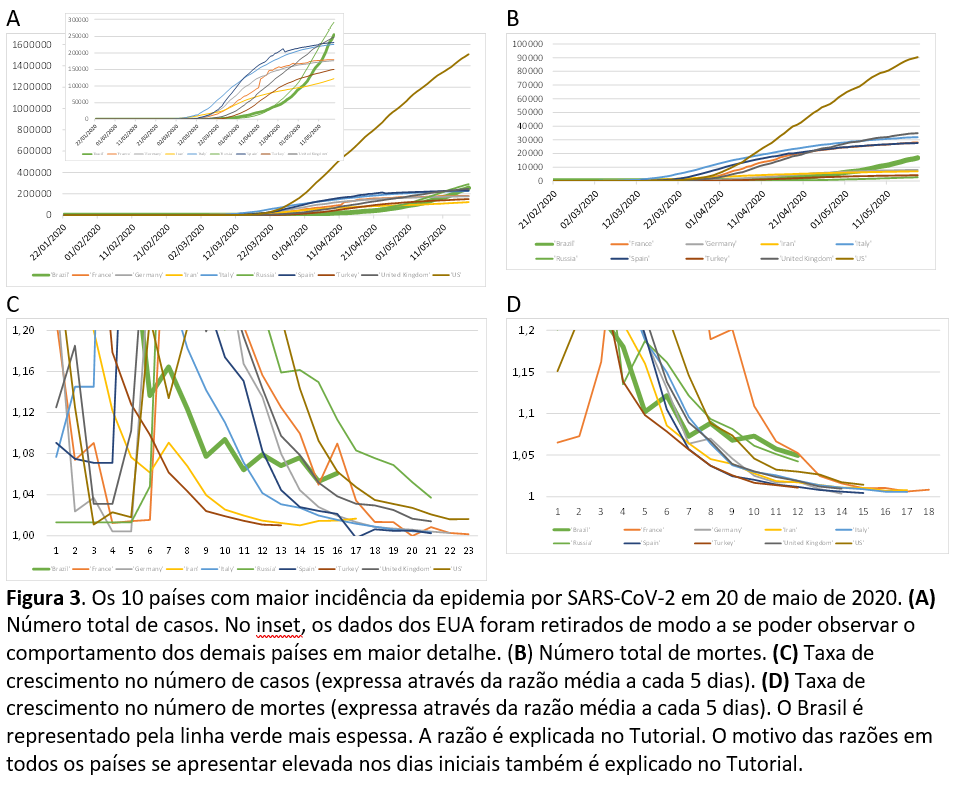
A resposta a esta pergunta é sim. O Brasil é o 3º ou 4º país em número de casos confirmados8, com 271.628 registros, correspondendo a 6% dos casos mundiais. Em segundo lugar se encontra a Rússia (299.941 casos – 6%) e, em primeiro, os Estados Unidos (1.569.659 casos – 32%). Figura 3A.
Pergunta 2: o número de mortes por COVID-19 no Brasil é significativo no panorama mundial?
A resposta é, novamente, sim. O Brasil encontra-se em 5º lugar com 17.971 mortes, representando, mais uma vez, 6% do total mundial. Figura 3B.
Pergunta 3: a taxa de crescimento no número de casos no Brasil se encontra dentro das taxas observadas em outros países?
Nos primeiros 50 dias da epidemia no Brasil, a taxa de crescimento se encontrava na média dos 10 países que mais têm casos atualmente (EUA, Rússia, Brasil Reino Unido, Espanha, Itália, França, Alemanha, Turquia, Irã). A partir de então, esta taxa tendeu a se estabilizar em torno de 1,06 a 1,07 (6% a 7% de crescimento diário), e agora, por volta do 85º dia da epidemia no Brasil, encontra-se esta mesma taxa, superando a dos demais 9 outros países citados (em termos comparativos, o 85º dia da França, dos EUA e da Rússia tinham taxas superiores às do Brasil, mas já se mostravam em franco declínio). Figura 3C.
Pergunta 4: a taxa de crescimento das mortes no Brasil se encontra dentro das taxas observadas em outros países?
A taxa de crescimento de mortes é a mais elevada entre os 10 países com maior número de casos na atualidade, além de não apresentar a tendência ao declínio que foi observada em outros locais. Figura 3D.
Pergunta 5: a porcentagem de mortes por COVID-19 entre os contaminados no Brasil se encontra dentro das porcentagens observadas nos demais países?
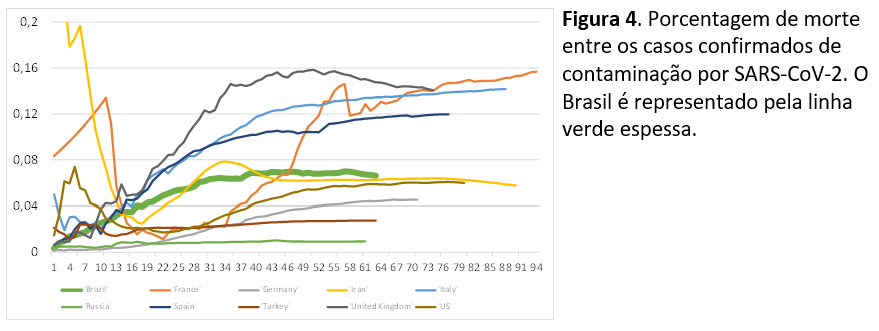
Sim, para o período relativo atual da epidemia no Brasil, a porcentagem de mortes se encontra em 6,5%, o que está na média entre os 10 países de maior número de casos para o período. Figura 4.
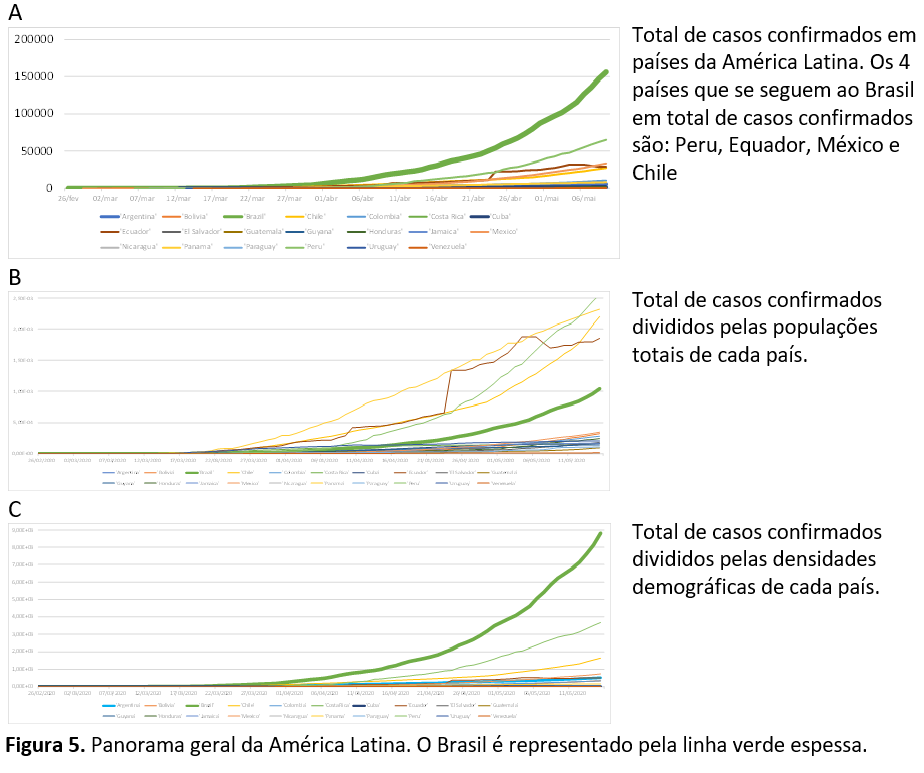
Pergunta 6: dentro da América Latina, o Brasil é o país com maior número de contaminações se feitos ajustes para a população total e para a densidade demográfica de cada país da região?
Sim. Se expresso em número de casos totais, o Brasil é o país com maior número de casos. Se feito o ajuste para a população total (não adequado, como é explicado no Tutorial), o Brasil passa a ser o 5º entre os 21 países. Se feito o ajuste para a densidade demográfica, o Brasil volta a assumir a primeira colocação (este ajuste é adequado, como explicado no Tutorial). Figura 5.
Cloroquina
Apesar de não ser o foco do presente texto as questões clínicas envolvendo o SARS-CoV-2 e a doença por este causada, a COVID-19, dada a situação na qual o país se encontra, acho que se torna oportuno vermos o que se têm acerca do uso da cloroquina para esta doença. Assim, apresento, abaixo, dois trechos extraídos de revisões em revistas científicas de extremo renome na área médica.
“Os médicos estão tratando pacientes numa falta de parsimônia inigualável, usando medicamentos como cloroquina, hidroxicloroquina, azitromicina, lopinavir-ritonavir e inibidores de interleucina-6 fora de seus usos indicados e aprovados, sem protocolos de estudo e com poucas evidências científicas que apóiem sua administração além da extrapolação a partir de estudos in vitro de suas propriedades antivirais e anti-inflamatórias. Além dos possíveis efeitos colaterais de medicamentos como a hidroxicloroquina e os inibidores da interleucina-6, que incluem arritmias cardíacas fatais e possível agravamento da infecção, respectivamente, a prescrição de medicamentos com base em relatos de caso faz pouco para ajudar a ciência avançar ou a nossa capacidade de combater futuras recorrências de coronavírus. … Nesses tempos de incerteza, os médicos são vítimas de erros cognitivos e inconscientemente confiam em experiências limitadas, sejam elas próprias ou de outras pessoas, em vez de investigações científicas”.(Zagury-Orly and Schwartzstein, 2020) – tradução livre.
“A hidroxicloroquina tem sido amplamente administrada a pacientes com Covid-19 sem evidência robusta que apoie seu uso … Examinamos a associação entre uso de hidroxicloroquina e intubação ou morte em um grande centro médico na cidade de Nova York. CONCLUSÕES. Neste estudo observacional envolvendo pacientes com Covid-19 que foram admitidos no centro hospitalar, a administração de hidroxicloroquina não foi associada a um risco nem reduzido nem aumentado do ponto final composto por intubação ou morte. Ensaios clínicos randomizados e controlados de hidroxicloroquina em pacientes com Covid-19 são precisos. (Financiamento: NIH)”. (Geleris et al., 2020) atualizado em 14 de maio – tradução livre.
Um breve (e simplificado) tutorial acerca de modelos em epidemiologia
O que é preciso ser considerado antes de iniciarmos uma análise direta dos dados?
Precisamos, inicialmente, ter uma noção de como os dados de uma epidemia podem se comportar. Isto, no fundo, é se ter um modelo contra o qual se fazem as comparações/previsões. Não é nosso objetivo, neste texto, fazer uma apresentação detalhada deste tipo de modelagem, contudo, para que as análises façam sentido, é preciso uma explicação mínima de parte do processo.
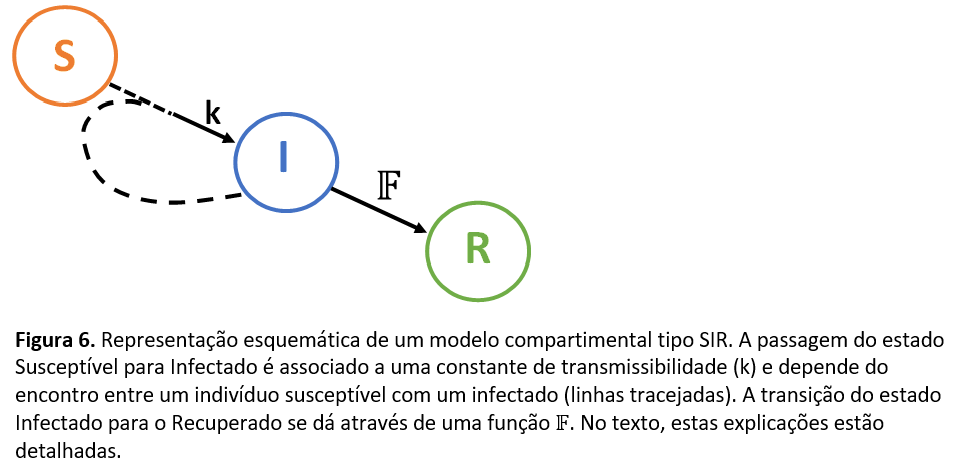
Como foi mencionado mais acima, um modelo simples de propagação de doenças infectocontagiosas possui três estados: os susceptíveis, os infectados e os recuperados. Como, geralmente, uma epidemia dura um tempo “curto” frente às variações demográficas de uma população, considera-se que a população total N não se altera, ou seja, a soma S+I+R tem um valor constante9. Também como mencionado, um individuo susceptível se torna infectado pelo contato com outro individuo infectado. Estas relações qualitativas são apresentadas na Figura 6. Abaixo, escrevo como um modelo compartimental (simples) lida com a variação da quantidade de infectados no tempo.
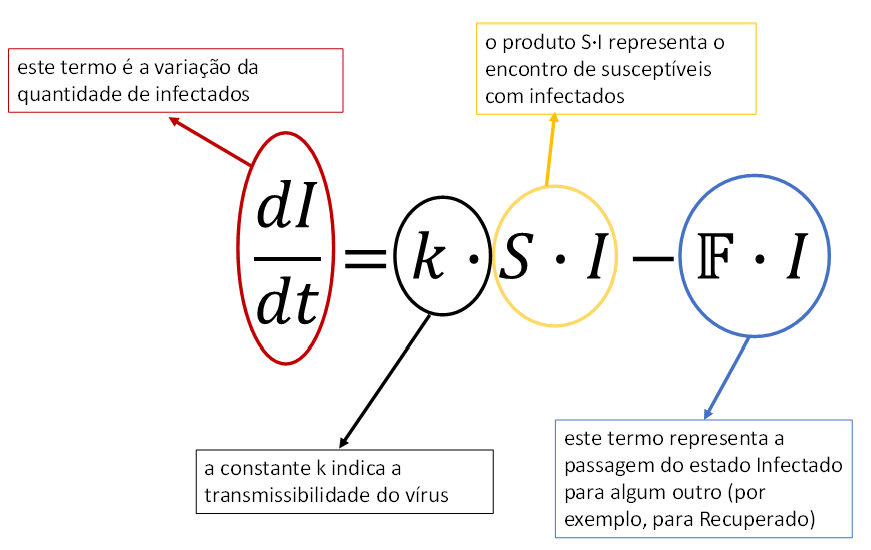
A função é uma função que pode ser simples ou complicada, porém não nos interessa. Não nos interessa pois estamos analisando as fases iniciais da propagação da epidemia, período no qual o número de infectados I é pequeno frente à população total, N. Assim, como I é pequeno, obviamente os estados dele decorrentes (como Recuperados) também são valores pequenos. Com isto, praticamente toda a população N se encontra no estado dos Susceptíveis. Como I é pequeno, o produto pode ser desprezado e, assim, a equação, para os períodos iniciais da propagação, pode ser aproximada por:
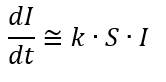
E esta equação tem, como solução:
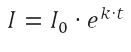
Sendo I0 a quantidade inicial de infectados e I a quantidade de infectados no tempo t. Note que como se trabalha com valores normalizados, S ≅ N = 1, e, assim, omiti este termo da equação.
Suponha que estejamos medindo o tempo em dias: dia zero, dia um, dia dois, etc.. Se soubermos o número de infectados num certo dia X e no dia seguinte, X+1, podemos fazer a razão:
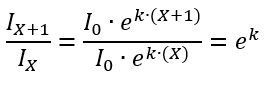
Como e é uma constante e k é outra constante, essa razão também é uma constante. Através dela podemos estimar duas coisas: (1) a constante k da taxa de crescimento do número de casos; (2) quanto tempo demorará para dobrar o número de casos que se tem num certo dia.
Além destas duas importantes estimativas que podemos fazer, existe uma vantagem adicional em se fazer a razão entre a quantidade de casos num dia em relação ao dia anterior: este valor (dado por ek na equação acima) é independente do tamanho total da população. Ou seja, se estamos diante de um país com 200 milhões de habitantes ou se estamos diante de um país com 30 milhões de habitantes, o valor da razão não depende destes números e, assim, podemos comparar países de diferentes populações. Voltaremos a este assunto mais adiante.
As curvas “total de casos” e “quantidade de infectados”
Um outro aspecto que deve ser deixado claro antes de se olhar para dados é a questão de qual conjunto de dados se está analisando. No contexto do espalhamento de uma doença infectocontagiosa, pode-se querer saber quantos indivíduos já foram contaminados ou pode-se querer saber quantos indivíduos estão contaminados num dado momento. O primeiro caso é, assim, uma função que sempre cresce ao longo do tempo, pois um indivíduo que foi contaminado entra na contagem e não mais sai dela, independentemente de haver se recuperado. Esta função somente irá parar de crescer quando toda a população tiver sido contaminada.
Por outro lado, a função dos indivíduos que estão contaminados num dado momento é diferente. Conforme o número de infectados e de recuperados aumenta, o número de susceptíveis diminui. Isso significa que aquele termo F, que ignoramos para os períodos iniciais da epidemia, se tonará importante na equação da variação do número de infectados. Como se observa, este termo é negativo, o que implica que com o aumento do número de infectados e diminuição de susceptíveis, em algum momento o termo F·I se torna maior que o termo k·S·I e, então, a quantidade de infectados começa a diminuir. Assim, diferentemente da função “total de contaminados”, a função “quantidade de infectados” tem um ápice seguido de um declínio. A Figura 7 ilustra estas duas funções.
Figura 7. Total de contaminados (linha preta), quantidade de infectados (linha azul) ao longo do tempo. Note que o total de contaminados é uma função sempre crescente enquanto a quantidade de infectados num dado instante atinge um ápice e cai. No inset, a razão explicada anteriormente.
Portanto, a expressão “achatamento da curva” se refere à função “quantidade de infectados” (linha azul na Figura 7).
Qual seria o correspondente a este achatamento da curva se estivéssemos observando a função “total de contaminados” (linha preta)? Como visto, o total de contaminados não irá parar de crescer até que toda a população tenha sido contaminada. Contudo, a taxa com que esse total cresce é dada pela função da variação dos infectados. Desta maneira, através da razão ilustrada mais acima, , pode-se estimar a contenção da propagação. Quanto mais próxima do valor “1” a razão estiver, significa que há cada vez menos casos de contaminação surgindo na população. Assim, o correspondente a “achatar a curva” azul da quantidade de infectados é, na função do total de contaminados, ter a razão próxima de 1.
Utilizando a razão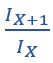 
para se ter uma estimativa do que irá ocorrer nos dias subsequentes
Vamos, agora, apresentar uma tabela para que se tenha uma noção do impacto dos valores da razão no que se pode esperar na quantidade de casos nos dias subsequentes a um determinado cálculo. Isto é importante pois, como os/as leitores/as já devem ter lido em outros locais, a razão, muitas vezes apresentada na forma de porcentagem de crescimento como, por exemplo, “6% de crescimento”, é um valor aparentemente pequeno. Isto pode dar a falsa impressão de que a doença se propaga lentamente. Vejamos.
Tabela 1. Fator multiplicador em função da razão na quantidade de casos.
Na primeira coluna da Tabela 1, temos valores da razão. Na segunda coluna, como estes valores seriam lidos em porcentagem. Assim, por exemplo, uma razão de 1,04 significa 4% de crescimento. Nas demais colunas tem-se o fator multiplicador em função do número de dias, indicados na segunda linha, após um certo cálculo da razão. Por exemplo, se, num determinado dia foram registrados 8.000 casos acumulados e a razão calculada foi de 1,05 (5%), projeta-se que após 10 dias haverá 13.040 casos (oito mil vezes um virgula sessenta e três).
Note como taxas aparentemente baixas, como 2%, resultam em valores altos após um período mais longo. No exemplo acima, se tivéssemos uma razão de 1,02, os 8.000 casos se transformariam em 26.240 após 60 dias, ou seja, mais que triplicariam.
As razões que vêm sendo observadas para o Brasil estão na faixa de 1,06 a 1,07 (realçadas na tabela), como se pode conferir na Figura 3C. Isso significa que mais ou menos a cada 10 dias, o número de casos duplica, e o mesmo se dá com o número de mortes. Desta maneira, entre o dia 17 de março, quando se registrou a primeira morte por COVID-19 no país até o dia 10 de maio, ocorreram 10.000 mortes. Entre o dia 10 e o dia em que este texto está sendo finalizado, 19 de maio, há 17.971 registros de mortes por COVID-19. Em 54 dias, ocorreram 10.000 mortes, e em 9 dias ocorreram mais 7.970, ou seja, em nove dias ocorreram quase 80% de novas mortes que nos cinquenta e quatro dias precedentes. Este é o impacto da propagação a uma taxa de 6% a 7%.
Modos adequados de visualizar e analisar os dados
A questão do tamanho populacional
Como foi dito mais acima, existe um potencial problema em se visualizar/analisar os dados devido a tamanhos diferentes de populações envolvidas. Por exemplo, a Argentina conta com 45 milhões de habitantes, enquanto o Brasil tem 210 milhões. Assim, não parece justo se comparar diretamente os valores de número de casos ou número de mortes nestes dois países. Contudo, como explico a seguir, estas comparações são, de fato, válidas.
Quando os gráficos de dados acerca do estado da pandemia no Brasil e em vários países foram apresentados, foi dito que a visualização/analise tendo-se o número de casos dividido pelo tamanho populacional é o modo menos adequado para o procedimento. Por que?
Considere o modelo básico de propagação de doenças infectocontagiosas apresentado mais acima. Nele, o termo de crescimento do número de infectados depende do produto S·I, o qual representa o encontro entre susceptíveis e infectados. Assim, como é óbvio para doenças infectocontagiosas, há o pressuposto do encontro entre indivíduos para a propagação da doença. Ao se querer corrigir a potencial distorção dos tamanhos populacionais dividindo-se o número de casos pelo total da população do país, assume-se que todos os indivíduos desta população estão em contato uns com os outros, como se estivessem, todos, numa única panela. E isto não é verdade.
Desta maneira, caso se queira fazer algum tipo de correção não muito elaborada nos dados, o mais correto é se dividir pela densidade populacional do país, pois, então, tem-se um índice de “proximidade” entre os indivíduos. Por esta razão é que os dados corrigidos para a densidade demográfica foram apresentados na Figura 5 para comparações entre os países da América Latina.
Como apontei acima, a suposta distorção nos dados brutos de número de casos é apenas potencial nas fases iniciais de uma pandemia. Isto se deve ao fato de que as epidemias locais se espalham, inicialmente, nos grandes centros urbanos, e as grandes cidades do mundo têm características demográficas bastante semelhantes em termos de organização urbana e densidade populacional. Assim, os dados brutos refletem, nestas fases iniciais, a transmissão em centros similares e a observação destes dados diretamente não compromete as conclusões a que se possa chegar nestas fases.
O artefato numérico dos primeiros dias da epidemia
Quando observamos as Figuras 3C e 3D, que apresentam as razões de contaminados e a de mortes, respetivamente, notamos que os dias iniciais parecem ter taxa de propagação extremamente elevadas as quais, posteriormente, decrescem. Encontram-se razoes acima de 2 em vários dias e em todos os países isto ocorre.
Uma análise equivocada é supor que a epidemia está sendo controlada e que, por isso, as taxas (as razões) diminuem, o que o vírus altera suas características de transmissibilidade, e, novamente, por isso as taxas declinam.
A perspectiva correta é que estas taxas (razões) elevadas nos dias iniciais nada mais são do que artefatos numéricos que ocorrem devido a dois fatores: (1) pequeno número de casos; (2) detecção de casos que já estavam na população, mas ainda não haviam se manifestado.
O fator (1) acima implica no seguinte. Imagine que haja, no segundo dia, 10 casos confirmados. No terceiro dia, surgem mais 8 casos, o que resulta numa razão de 18/10 = 1,8. Ou seja, basicamente esse número nos diz que o número de casos praticamente dobrará de um dia para o seguinte. Mas, isso é meramente o efeito de haver poucos casos registrados. Esses mesmos 8 casos num total de 100 anteriores resultaria numa razão de 108/100 = 1,08, um valor ainda alto, porém bem mais factível. E, ao fator (1), combina-se o fator (2). A propagação de doenças infectocontagiosas se dá através de algum tipo de contato, e ao se calcularem as taxas de crescimento (como a razão), fica embutida a ideia de que indivíduos contaminados fizeram surgir os novos casos. Porém, no inicio da epidemia, não é isto que está ocorrendo. A maior parte dos casos que surgem nos primeiros dias são casos que já estavam na população, mas ainda não haviam sido detectados. Assim, estes casos não têm, necessariamente, a origem nos casos já registrados e, ao “surgirem”, inflacionam as taxas de crescimento da epidemia. Portanto, como se nota nos gráficos apresentados, somente quando os dias iniciais se vão e o número total de casos fica “grande” é que cálculos simples das taxas, como a razão, passam a fazer sentido preditivo e de diagnóstico das políticas públicas.
Dados em escala linear e em escala logarítmica
A Figura 8 ilustra a situação hipotética de espalhamento de uma doença infectocontagiosa em dois locais (países, por exemplo) diferentes. O painel A apresenta os dados em escala linear, enquanto o painel B apresenta estes mesmos dados em escala logarítmica. Uma vez que são os mesmos dados, a informação dada pelo painel A é a mesma que a dada pelo painel B. Contudo, visualmente, o impacto destes painéis é bem diverso.
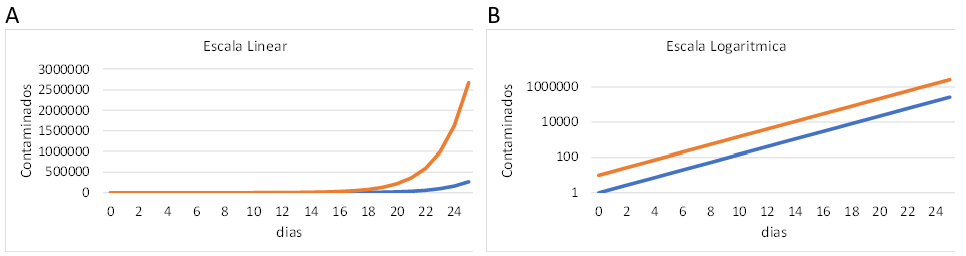
Figura 8. Simulação das fases iniciais de espalhamento de uma doença infectocontagiosa em duas localidades diferentes. (A) escala linear; (B) escala logarítmica. As simulações tiveram a mesma constante de espalhamento (0,5 por dia) e, na localidade representada pela linha azul, há inicialmente 1 infectado, enquanto na localidade representada pela linha laranja, há 10 infectados no momento inicial.
Nós, seres humanos, avaliamos os contextos de forma basicamente linear. Assim, ao observar o painel B, a sensação gerada é de que a doença é mais acentuada no país laranja, porém “apenas pouco mais acentuada”. Mas, observando o painel A, tem-se a verdadeira diferença entre o país laranja e o país azul: há dez vezes mais casos no laranja que no azul. Por outro lado, exatamente por esse nosso viés de avaliação linear, ao observarmos o painel A temos a impressão de que a doença se espalha muito mais rapidamente no país laranja que no país azul. Agora, ao observarmos os dados em escala logarítmica, percebemos que as taxas de espalhamento são as mesmas nos dois países.
Como se pode haver depreendido de tudo o que já foi apresentado nesta secção, o espalhamento de uma doença infectocontagiosa nas fases iniciais de uma epidemia tem um caráter multiplicativo. Esse caráter multiplicativo faz com que, em uma escala linear, algumas localidades tenham um crescimento no número de casos que se torna muito e progressivamente mais elevado que em outras regiões. Contudo, a função logaritmo é uma função que lida, exatamente, com multiplicações e, assim, numa escala logarítmica, o processo multiplicativo se torna linear, facilitando a visualização das diferentes regiões a despeito da diferença no número de casos de cada uma. Além disso, curvas paralelas em escala logarítmica indicam que os processos têm a mesma taxa de crescimento.
Por estes motivos é que se dá preferência a apresentar os dados em escala logarítmica. Contudo, se você não tem familiaridade com este tipo de representação gráfica, recomenda-se que você faça as duas, linear e logarítmica, de modo a poder manter a intuição acerca de quanto a doença já se espalhou nas diferentes localidades (linear) e de quão rapidamente ela se espalha nas diferentes localidades (logarítmica).
A título de exemplo, reproduzo, na Figura 9A, o gráfico de total de contaminados ajustados para a densidade populacional nos países da América Latina, em escala linear (Figura 5C) e, em 9B, os mesmos dados em escala logarítmica. Note como, em 9B, podemos ter uma melhor percepção acerca da rapidez do espalhamento da doença nos diferentes países, o que não é possível em 9A.
Figura 9. Total de casos confirmados divididos pelas respectivas densidades demográficas de países da América Latina. (A) Escala linear. (B) Escala logarítmica.
Termino, aqui, este breve e simplificado tutorial acerca de modelos para as fases iniciais de propagação de uma doença infectocontagiosa, e espero que este tutorial possa ser de ajuda para o melhor entendimento dos dados que vem sendo apresentados diariamente acerca da pandemia causada pelo SARS-CoV-2.
*José Guilherme Chaui-Berlinck é professor livre-docente do Departamento de Fisiologia do Instituto de Biociências da USP.
Referências interessantes de revisão
(Bar-On et al., 2020) – Apresentam um grande resumo dos principais aspectos do vírus, da doença e da pandemia. Vale a pena consultar este artigo.
(Mamun et al., 2020) – Outro breve resumo dos principais achados em termos da pandemia até o momento
(Fiorillo et al., 2020) – Tempo de persistência do SARS-CoV-2 em diferentes superfícies e temperaturas.
(Chin et al., 2020) – Viabilidade de SARS-CoV-2 em diferentes superfícies e diferentes temperaturas.
(Netz, 2020) – Física de gotículas e aerossóis. Vale a pena consultar este artigo, porém é necessário um certo background de matemática.
Referências Bibliográficas
Anderson, E. L., Turnham, P., Griffin, J. R. and Clarke, C. C. (2020). Consideration of the Aerosol Transmission for COVID‐19 and Public Health. Risk Anal. 40, 902–907.
Anfinrud, P., Bax, C. E., Stadnytskyi, V. and Bax, A. (2020). Could SARS-CoV-2 be transmitted via speech droplets? medRxiv 2020.04.02.20051177.
Bar-On, Y. M., Flamholz, A., Phillips, R. and Milo, R. (2020). SARS-CoV-2 (COVID-19) by the numbers. Elife 9,.
Barr, G. D. (2020). The Covid-19 Crisis and the need for suitable face masks for the general population. Chinese J. Med. Res. 3, 28–31.
Brurberg, K. G. (2020). Transmission of SARS-CoV-2 via contact and droplets, 1st update – a rapid review. Nor. Inst. Public Heal. May 7, 1–17.
Chin, A. W. H., Chu, J. T. S., Perera, M. R. A., Hui, K. P. Y., Yen, H.-L., Chan, M. C. W., Peiris, M. and Poon, L. L. M. (2020). Stability of SARS-CoV-2 in different environmental conditions. The Lancet Microbe 0–4.
Cipriano, M., Ruberti, E. and Giacalone, A. (2020). Gastrointestinal Infection Could Be New Focus for Coronavirus Diagnosis. Cureus 12,.
Dancer, S. J., Tang, J. W., Marr, L. C., Miller, S., Morawska, L. and Jimenez, J. L. (2020). Putting a balance on the aerosolization debate around SARS-CoV-2. J. Hosp. Infect.
Deng, W., Bao, L., Gao, H. and Qin, C. (2020). Ocular conjunctival inoculation of SARS-CoV-2 can cause mild COVID-19 in Rhesus macaques. bioRxiv prepriint,.
Eikenberry, S. E., Mancuso, M., Iboi, E., Phan, T., Eikenberry, K., Kuang, Y., Kostelich, E. and Gumel, A. B. (2020). To mask or not to mask: Modeling the potential for face mask use by the general public to curtail the COVID-19 pandemic. Infect. Dis. Model. 5, 293–308.
Esposito, S., Principi, N., Leung, C. C. and Migliori, G. B. (2020). Universal use of face masks for success against COVID-19: evidence and implications for prevention policies. Eur. Respir. J. 2001260.
Fiorillo, L., Cervino, G., Matarese, M., D’Amico, C., Surace, G., Paduano, V., Fiorillo, M. T., Moschella, A., La Bruna, A., Romano, G. L., et al. (2020). COVID-19 Surface Persistence: A Recent Data Summary and Its Importance for Medical and Dental Settings. Int. J. Environ. Res. Public Health 17, 3132.
Galbadage, T., Peterson, B. M. and Gunasekera, R. S. (2020). Does COVID-19 Spread Through Droplets Alone? Front. Public Heal. 8, 1–4.
Geleris, J., Sun, Y., Platt, J., Zucker, J., Baldwin, M., Hripcsak, G., Labella, A., Manson, D. K., Kubin, C., Barr, R. G., et al. (2020). Observational Study of Hydroxychloroquine in Hospitalized Patients with Covid-19. N. Engl. J. Med. NEJMoa2012410.
Hadei, M., Hopke, P. K., Jonidi, A. and Shahsavani, A. (2020). A Letter about the Airborne Transmission of SARS-CoV-2 Based on the Current Evidence. Aerosol Air Qual. Res. 20, 911–914.
He, X., Lau, E. H. Y., Wu, P., Deng, X., Wang, J., Hao, X., Lau, Y. C., Wong, J. Y., Guan, Y., Tan, X., et al. (2020). Temporal dynamics in viral shedding and transmissibility of COVID-19. Nat. Med.
Hsiao, T.-C., Chuang, H.-C., Griffith, S. M., Chen, S.-J. and Young, L.-H. (2020). COVID-19: An Aerosol’s Point of View from Expiration to Transmission to Viral-mechanism. Aerosol Air Qual. Res. 905–910.
Kai, D., Goldstein, G., Morgunov, A., Nangalia, V. and Rotkirch, A. (2020). Universal Masking is Urgent in the COVID-19 Pandemic: SEIR and Agent Based Models, Empirical Validation, Policy Recommendations. arXiv.
La Rosa, G., Bonadonna, L., Lucentini, L., Kenmoe, S. and Suffredini, E. (2020). Coronavirus in water environments: Occurrence, persistence and concentration methods – A scoping review. Water Res. 179, 115899.
Lamers, M. M., Beumer, J., van der Vaart, J., Knoops, K., Puschhof, J., Breugem, T. I., Ravelli, R. B. G., Paul van Schayck, J., Mykytyn, A. Z., Duimel, H. Q., et al. (2020). SARS-CoV-2 productively infects human gut enterocytes. Science (80-. ). 1669, eabc1669.
Li, D., Zhao, M. Y. and Hsern, M. T. T. (2020). What makes a foodborne virus: comparison between coronaviruses with human noroviruses. Curr. Opin. Food Sci. pre–proof, 108709.
Mamun, M. Al, Mannoor, K., Shirin, T., Flora, M. S., Qadri, F., Ren, L. and Wang, J. (2020). A snapshot on COVID-19: A review. 1–16.
McDermott, C. V., Alicic, R. Z., Harden, N., Cox, E. J. and Scanlan, J. M. (2020). Put a lid on it: Are faecal bio-aerosols a route of transmission for SARS-CoV-2? J. Hosp. Infect. pre–proof,.
Morawska, L. and Cao, J. (2020). Airborne transmission of SARS-CoV-2: The world should face the reality. Environ. Int. 139, 105730.
Netz, R. R. (2020). Lifetime of virion-containing droplets diffusing and evaporating in air. Pers. notes.
Pan, Y., Zhang, D., Yang, P., Poon, L. L. M. and Wang, Q. (2020). Viral load of SARS-CoV-2 in clinical samples. Lancet Infect. Dis. 20, 411–412.
Peters, A., Parneix, P., Otter, J. and Pittet, D. (2020). Putting some context to the aerosolization debate around SARS-CoV-2. J. Hosp. Infect. pre–proof,.
van Doremalen, N., Bushmaker, T., Morris, D. H., Holbrook, M. G., Gamble, A., Williamson, B. N., Tamin, A., Harcourt, J. L., Thornburg, N. J., Gerber, S. I., et al. (2020). Aerosol and Surface Stability of SARS-CoV-2 as Compared with SARS-CoV-1. N. Engl. J. Med. 382, 1564–1567.
Wong, M., Huang, J., Lai, C., Ng, R., Chan, F. and Chan, P. K. S. (2020). The detection of novel coronavirus in faecal specimens of patients with confirmed COVID-19 : a systematic review and meta-analysis. Lancet Gastroenterol. Hepatol. ms draft,.
Xiao, F., Tang, M., Zheng, X., Liu, Y., Li, X. and Shan, H. (2020). Evidence for Gastrointestinal Infection of SARS-CoV-2. Gastroenterology 158, 1831-1833.e3.
Zagury-Orly, I. and Schwartzstein, R. M. (2020). Covid-19 — A Reminder to Reason. N. Engl. J. Med. NEJMp2009405.
Notas
[1] SARS: Severe Acute Respiratory Syndrome (síndrome respiratória aguda severa); CoV-2: coronavirus tipo 2.
[2] Um fômite ou fómite é qualquer objeto inanimado ou substância capaz de absorver, reter e transportar organismos contagiantes ou infecciosos (de germes a parasitas), de um indivíduo a outro. – Fonte: wikipedia.pt.
[3] Cabe notar que Lidia Morawska, citada no início deste parágrafo, faz parte dos autores deste artigo.
[4] Os autores ainda discutem que para o potencial receptor do material lançado, a máscara diminui o raio do ar a ser inspirado pois funciona como um difusor invertido.
[5] Estes modelos nos quais o espaço passa a ser um dos componentes são, em geral, impossíveis de serem resolvidos de maneira analítica e seus resultados são oriundos de simulações numéricas.
[6] “Agent Based Modelling” é um modelo de simulação numérica que envolve o deslocamento dos indivíduos simulados.
[7] Os dados aqui apresentados graficamente vão até o dia 18/maio. Os dados apresentados pontualmente dizem respeito ao dia 19 de maio.
[8] A indecisão entre o 3º e o 4º posto decorre do horário de atualização dos dados pelos diferentes países.
[9] Note que, para finalidades de simplificação, podemos colocar os indivíduos que morrem como parte dos recuperados, sem alterar a dinâmica do processo, uma vez que a população total se mantém constante.
